Answer:
the maximum distance of rotation can he stand without sliding is 1.77 m
Step-by-step explanation:
given information:
angular velocity , ω = 1.58 rad/s
static friction, μs = 0.45
now we calculate the vertical force
N - W = 0, N is normal force and W is weight
N = W
= m g
next, for the horizontal force we only have frictional force, thus
F(friction) = m a
μs N = m a
μs m g = m a
a = μs g,
now we have to find the acceleration which is both translation and cantripetal.
a =
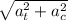
 is the acceleration for translation
is the acceleration for translation
 = 0
= 0
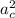 is centripetal acceleration
is centripetal acceleration
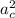 = ω^2r
= ω^2r
therefore,
a =
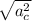
=
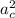
= ω^2r
Now, to find the radius, substitute the equation into the following formula
a = μs g
ω^2r = μs g
r = μs g / ω^2
= (0.45 x 9.8) / (1.58)
= 1.77 m