Answer:
The satellite has a period of 204.90 days
Step-by-step explanation:
The period can be determine by means of Kepler's third law:
 (1)
(1)
Where T is the period of revolution and r is the radius.

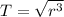 (2)
(2)
The distance between the moon and the Earth has a value of 384400 km, therefore:


Finally, equation 2 can be used:
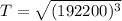
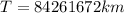
However, the period can be expressed in days, to do that it is necessary to make the conversion from kilometers to astronomical units:
An astronomical unit (AU) is the distance between the Earth and the Sun (
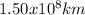 )
)
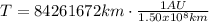 ⇒
⇒
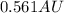
But 1 year is equivalent to 1 AU according to Kepler's third law, since 1 year is the orbital period of the Earth.
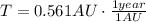 ⇒
⇒
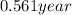
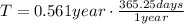 ⇒
⇒
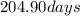
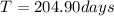
Hence, the satellite has a period of 204.90 days.