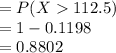Answer:
0.8802
Explanation:
given that the Police estimate that 84% of drivers wear their seatbelts.
when they stop 140 cars, no of trials = no of cars checked = 140
Each car is independent of the other
Hence X no of cars with drivers wearing seat belts is binomial with p = 0.85
Required probability =
the probability they find at least 27 drivers not wearing their seatbelts
Since normal approximation is required we can approximate to
X is Normal with mean = np =
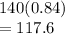
std dev =

Required probability =atelast 27 drivers not wearing their seatbelts
= P(X>(140-27))
= P(X>113)