Question

A recent study was conducted to determine the curing efficiency (time to harden) of dental composites (resins for the restoration of damaged teeth) using two different types of lights. Independent random samples of lights were obtained and a certain composite was cured for 40 seconds. The depth of each cure (in mm) was measured using a penetrometer. The summary statistics for the Halogen light were n_1 = 10, x_1 = 5.35, and s_1 = 0.7. The summary statistics for the LuxOMax light were n_2 = 10, x_2 = 3.90, and s_2 = 0.8. Assume the underlying populations are normal, with equal variances. a. The maker of the Halogen light claims that they produce a larger cure depth after 40 seconds than LuxOMax lights. Is there any evidence to support this claim? Use alpha = 0.01. b. Construct a 99% confidence interval for the difference in population mean cure depths.

Answer 1

(1.4328, 1.622)

Claim is supported by evidence.

Explanation:

Given that a recent study was conducted to determine the curing efficiency (time to harden) of dental composites (resins for the restoration of damaged teeth) using two different types of lights.

Let X be the halogen and y the Luxomax light

`H_0: \bar x =\bar y\\H_a: \bar x > \bar Y`

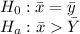
(Two tailed test)

we are given data as:

Group Group One Group Two

Mean 5.3500 3.9000

SD 0.7000 0.8000

SEM 0.2214 0.2530

N 10 10

The mean of Group One minus Group Two equals 1.4500

Std error for difference = 0.336

Test statistic t=4.3135

df = 18

p value = 0.0004

Since p <0.01 at 1% level, reject H0

There is significant difference and hence the claim is valid.

There is evidence to support this claim at 1% significance level

Margin of error =1.172

99% confidence interval =
`(1.45-1.172, 1.45+1.172)\\\\=(1.4328, 1.622)`