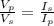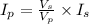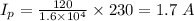Answer:
(A) 18667 turns
(B) 1.7 A
Solution:
As per the question:
Voltage at which the electricity is distributed,
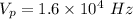
Frequency of the oscillating voltage, f = 60 Hz
Step down voltage,
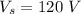
No. of turns in the secondary coil,
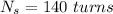
Current in the secondary coil,
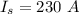
Now,
(A) To calculate the primary no. of turns, we use the relation:
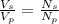
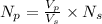
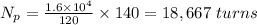
(B) To calculate the current in the primary coil,
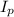 , we use the relation:
, we use the relation: