Question

What is the distance from axis about which a uniform, balsa-wood sphere will have the same moment of inertia as does a thin-walled, hollow, lead sphere of the same mass and radius R, with the axis along a diameter, to the center of the balsa-wood sphere?

Answer 1

`D_(s)` ≈ 2.1 R

Step-by-step explanation:

The moment of inertia of the bodies can be calculated by the equation

I = ∫ r² dm

For bodies with symmetry this tabulated, the moment of inertia of the center of mass

Sphere
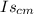`Is_(cm)` = 2/5 M R²

Spherical shell
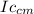`Ic_(cm)` = 2/3 M R²

The parallel axes theorem allows us to calculate the moment of inertia with respect to different axes, without knowing the moment of inertia of the center of mass

I =
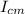`I_(cm)` + M D²

Where M is the mass of the body and D is the distance from the center of mass to the axis of rotation

Let's start with the spherical shell, axis is along a diameter

D = 2R

Ic =
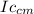`Ic_(cm)` + M D²

Ic = 2/3 MR² + M (2R)²

Ic = M R² (2/3 + 4)

Ic = 14/3 M R²

The sphere

Is =
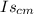`Is_(cm)` + M [
`D_(s)`²

Is = Ic

2/5 MR² + M
`D_(s)`² = 14/3 MR²

`D_(s)`² = R² (14/3 - 2/5)

`D_(s)` = √ (R² (64/15)

`D_(s)` = 2,066 R