Question

A small, 0.10 kg cart is moving at 1.54 m/s when it collides with a larger 1.52 kg cart at rest. After the elastic collision, the small cart recoils (i.e. bounces off the larger cart and travels in the opposite direction) at a speed of 0.76 m/s.(a) What is the magnitude (absolute value) of the change in momentum for the small cart? kg m/s(b) What is the speed (absolute value of the velocity) of the larger cart after the collision? m/s

Answer 1

a. the absolute value of the change in the momentum of the small car is 0.078

b. the velocity of the larger car after the collision is 0.1513 m/s

Step-by-step explanation:

The linear momentum P is calculated as:

P = MV

Where M is the mass and V the velocity

Therefore, for calculated the change of the linear momentum of the small cart, we get:

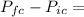`P_(fc)-P_(ic) =`ΔP

where
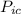`P_(ic)` in the inicial momentum and
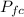`P_(fc)` is the final momentum of the small cart. Replacing the values, we get:

0.10 kg (0.76) -0.10(1.54) = -0.078 kg m/s

The absolute value: 0.078 kg m/s

On the other hand, using the law of the conservation of linear momentum, we get:

`P_i = P_f`

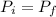
Where
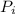`P_i` is the linear momentum of the sistem before the collision and
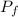`P_f` is the linear momentum after the collision.

`P_i=P_(ic)\\P_f=P_(fc) + P_(ft)`

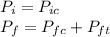
Where
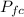`P_(fc)` is the linear momentum of the small cart after the collision and
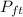`P_(ft)` is the linear momentum of the larger cart after the collision

so:

(0.10 kg)(1.54 m/s) = (0.10 kg)(-0.76 m/s) + (1.52 kg)(V)

Note: we choose the first direction of the small car as positive.

Solving for V:

`(0.10(1.54)+0.10(0.76))/(1.52) = V`

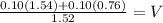
V = 0.1513 m/s