Question

A bank wishes to estimate the mean credit card balance owed by its customers. The population standard deviation is estimated to be $300. If a 98 percent confidence interval is used and an interval of $78 is desired, how many customers should be sampled?A. 725B. 80C. 57D. 320

Answer 1

Answer: B. 80

Explanation:

We know that the formula to find the sample size is given by :-

`n=((z^*\cdot\sigma)/(E))^2`

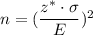
, where
`\sigma` = population standard deviation.

E= margin of error

z*= Two -tailed critical z-value

Given : Confidence level = 98% =0.98

`\alpha=1-0.98=0.02`

Population standard deviation :
`\sigma=300`

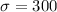
Also, from z-table for
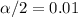`\alpha/2=0.01` (two tailed ), the critical will be =
`z^*=2.326`

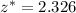
Then, the required sample size must be :

`n=((2.326\cdot300)/(78))^2\\\\ n=(8.94615)^2\\\\ n=80.0336686391\approx80` [To the nearest option]

Hence, the required sample size = 80

Hence, the correct option is option B. 80