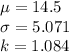Question

A statistician uses Chebyshev's Theorem to estimate that at least 15 % of a population lies between the values 9 and 20. Use this information to find the values of the population mean, μ , and the population standard deviation σ.

Answer 1

\mu = 14.5\\

\sigma = 5.071\\

k = 1.084

Explanation:

given that a statistician uses Chebyshev's Theorem to estimate that at least 15 % of a population lies between the values 9 and 20.

i.e. his findings with respect to probability are

`P(9<x<20) \geq 0.15\\P(|x-14.5|<5.5) \geq 0.15`

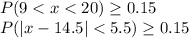
Recall Chebyshev's inequality that

`P(|X-\mu |\geq k\sigma )\leq {\frac {1}{k^(2)}}\\P(|X-\mu |\leq k\sigma )\geq 1-{\frac {1}{k^(2)}}\\`

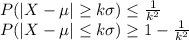
Comparing with the Ii equation which is appropriate here we find that

`\mu =14.5`

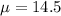
Next what we find is

`k\sigma = 5.5\\1-(1)/(k^2) =0.15\\(1)/(k^2)=0.85\\k=1.084\\1.084 (\sigma) = 5.5\\\sigma = 5.071`

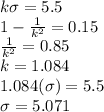
Thus from the given information we find that

`\mu = 14.5\\\sigma = 5.071\\k = 1.084`