Answer:
a = 9.94 m/s²
Step-by-step explanation:
given,
density at center= 1.6 x 10⁴ kg/m³
density at the surface = 2100 Kg/m³
volume mass density as function of distance
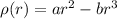
r is the radius of the spherical shell
dr is the thickness
volume of shell
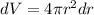
mass of shell
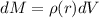

now,
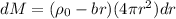
integrating both side
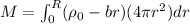

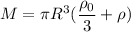
we know,
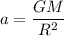
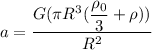

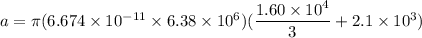
a = 9.94 m/s²