Question

At the Indianapolis 500, you can measure the speed of cars just by listening to the difference in pitch of the engine noise between approaching and receding cars. Suppose the sound of a certain car drops by a factor of 2.40 as it goes by on the straightaway. How fast is it going? (Take the speed of sound to be 343 m/s.)

Answer 1

To develop this problem it is necessary to apply the concepts related to the Dopler effect.

The equation is defined by

`f_i = f_0 (c)/(c+v)`

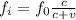
Where

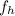`f_h`= Approaching velocities

`f_i`= Receding velocities

c = Speed of sound

v = Emitter speed

And

`f_h = f_0 (c)/(c+v)`

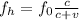
Therefore using the values given we can find the velocity through,

`(f_h)/(f_0)=(c-v)/(c+v)`

`v = c((f_h-f_i)/(f_h+f_i))`

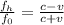
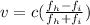
Assuming the ratio above, we can use any f_h and f_i with the ratio 2.4 to 1

`v = 353((2.4-1)/(2.4+1))`

`v = 145.35m/s`

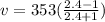
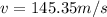
Therefore the cars goes to 145.3m/s