To develop this problem it is necessary to apply the concepts related to the Dopler effect.
The equation is defined by
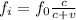
Where
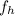 = Approaching velocities
= Approaching velocities
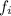 = Receding velocities
= Receding velocities
c = Speed of sound
v = Emitter speed
And
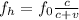
Therefore using the values given we can find the velocity through,
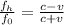
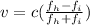
Assuming the ratio above, we can use any f_h and f_i with the ratio 2.4 to 1
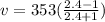
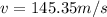
Therefore the cars goes to 145.3m/s