Question

What is the equation of a quadratic graph with a focus of (-4,17/8) and a detric of y=15/8 answer

Answer 1

keeping in mind that the vertex is between the focus point and the directrix, in this cases we have the focus point above the directrix, meaning is a vertical parabola opening upwards, Check the picture below, which means the "x" is the squared variable.

now, the vertical distance from the focus point to the directrix is
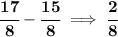`\bf \cfrac{17}{8}-\cfrac{15}{8}\implies \cfrac{2}{8}` , which means the distance "p" is half that or 1/8, and is positive since it's opening upwards.

since the vertex is 1/8 above the directrix, that puts the vertex at
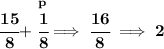`\bf \cfrac{15}{8}+\stackrel{p}{\cfrac{1}{8}}\implies \cfrac{16}{8}\implies 2` , meaning the y-coordinate for the vertex is 2.

`\bf \textit{vertical parabola vertex form with focus point distance} \\\\ 4p(y- k)=(x- h)^2 \qquad \begin{cases} \stackrel{vertex}{(h,k)}\qquad \stackrel{focus~point}{(h,k+p)}\qquad \stackrel{directrix}{y=k-p}\\\\ p=\textit{distance from vertex to }\\ \qquad \textit{ focus or directrix}\\\\ \stackrel{`

`\bf \begin{cases} h=-4\\ k=2\\ p=(1)/(8) \end{cases}\implies 4\left((1)/(8) \right)(y-2)=[x-(-4)]^2\implies \cfrac{1}{2}(y-2)=(x+4)^2 \\\\\\ y-2=2(x+4)^2\implies \blacktriangleright y = 2(x+4)^2+2 \blacktriangleleft`