Explanation:
Given that, Speed of the automobile, v = 55 km/h = 15.27 m/s
Diameter of the tire, d = 77 cm
Radius, r = 0.385 m
(a) Let
 is the angular speed of the tires about their axles.
is the angular speed of the tires about their axles.
The relation between the linear speed and the angular speed is given by :
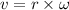
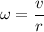
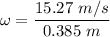
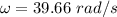
(b) Number of revolution,
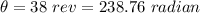
Final angular speed of the car,

Initial angular speed,
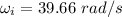
Let
 is the angular acceleration of the car. Using third equation of rotational kinematics as :
is the angular acceleration of the car. Using third equation of rotational kinematics as :
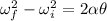
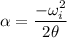
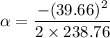
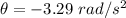
(c) Let d is the distance covered by the car during the braking. It is given by :
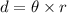
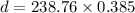
d = 91.92 meters