Question

A 5.0 g coin is placed 15 cm from the center of a turntable. The coin has static and kinetic coefficients of friction with the turntable surface of μs = 0.70 and μk = 0.50. The turntable very slowly speeds up.

Answer 1

Angular speed will reach 6.833rad/s before the coin starts slipping

Step-by-step explanation:

There is no question but I'll asume the common one: Calculate the speed of the turntable before the coin starts slipping.

With a sum of forces:

`Ff = m*a`

`Ff=m*V^2/R`

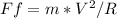
At this point, friction force is maximum, so:

`\mu*N=m*V^2/R`

`\mu*m*g=m*V^2/R`

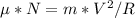
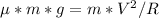
Solving for V:

`V=√(\mu*g*R)`

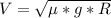
V=1.025 m/s

The angular speed of the turntable will be:

ω = V/R = 6.833 rad/s This is the maximum speed it can reach before the coin starts slipping.