Question

Two pipes are connected to the same tank. When working together., they can fill the tank in 10hrs. The larger pipe, working alone, can fill the tank in 15 hrs less time than the smaller one. How long would the smaller one take, working alone, to fill the tank

Answer 1

30 hours

Explanation:

Let the small pipe take time "t" to fill up the tank alone

Since larger pipe takes 15 HOURS LESS, so it will take "t - 15" time to fill up the tank alone

Let the whole tank be equal to "1" and each pipe fills up a fraction of the tank.

Smaller Pipe fills up 10/t, and

Larger Pipe fills up 10/(t-15)

Totalling "1". So we can write:

`(10)/(t)+(10)/(t-15)=1`

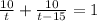
Now, we solve for t. First, we multiply whole equation by (t)(t-15), to get:

`t(t-15)*[(10)/(t)+(10)/(t-15)=1]\\(t-15)(10)+10t=t(t-15)`

Now we multiply out and get a quadratic and solve by factoring. Shown below:

`(t-15)(10)+10t=t(t-15)\\10t-150+10t=t^2-15t\\20t-150=t^2-15t\\t^2-35t+150=0\\(t-30)(t-5)=0\\t=5,30`

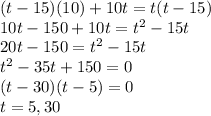
Since, this time is for the smaller pipe (which takes longer than 15 hours), so we disregard t = 5 and take t = 30 as our solution. So,

Smaller pipe takes 30 hours to fill up the tank alone