Question

The beta decay of cesium-137 has a half-life of 30.0 years. How many years must pass to reduce a 24 mg sample of cesium 137 to 6.0 mg?

Answer 1

60.0 years must pass to reduce a 24 mg of cesium 237 to 6.0 mg

Step-by-step explanation:

For radioactive decay of a radioactive nuclide-

`N_(t)=N_(0)((1)/(2))^{(\frac{t}{t_{(1)/(2)}})}`

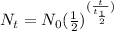
Where,
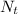`N_(t)` is amount of radioactive nuclide after "t" time , N_{0} is initial amount of radioactive nuclide and
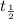`t_{(1)/(2)}` is half-life of radioactive nuclide

Here N_{0} = 24 mg, N_{t} = 6.0 mg and
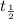`t_{(1)/(2)}` = 30.0 years

So,
`6.0mg=24mg* ((1)/(2))^{((t)/(30.0years))}`

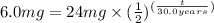
or,
`t=60.0years`

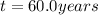
So 60.0 years must pass to reduce a 24 mg of cesium 237 to 6.0 mg