Answer:
skew lines
Explanation:
we are given 2 lines in parametric form as
L1:x=18+6t,y=7+3t,z=13+3t and L2:x=−14+7ty=−12+5tz=−8+6t
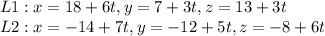
If the lines intersect then the two points must be equal for one value of t.
Let us try equating x,y and z coordinate.
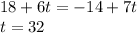
when we equate y coordinate we get
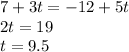
Since we get two different t we find that these two lines cannot intersect.
Comparing direction ratios we have
I line has direction ratios as (6,3,3) and second line (7,5,6)
These two are not proportional and hence not parallel
So these lines are skew lines