Question

American General offers a 7-year ordinary annuity with a guaranteed rate of 6.35% compounded annually. How much should you pay for one of these annuities if you want to receive payments of $10,000 annually over the 7-year period?

Answer 1

$ 55135.978

Explanation:

At most, the present value of annuity must be paid. So we must find the present value of the annuity

Given in the problem, we have:

Periodic Payment = PMT = $10000

Rate of interest annually = i = 6.35 %=
`(6.35)/(100)`=0.0635

no. of periods= n=7

So to solve this, we need to use the present value formula:

Present Value = Periodic payment
`(1-(1+rate.of.interest)^(-n) )/(rate.of.interest)`

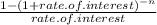
Present Value = PMT
`(1-(1+i)^(-n) )/(i)`

Present value = 10000
`(1-(1+0.0635)^(-7) )/(0.0635)`

Present Value =10000
`(0.35011)/(0.0635)`

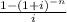
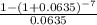
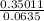
Present Value =10000 (5.5135978)

Present value= $ 55135.978

Which is the amount that must be paid at most to get annuities such that $10,000 annually over the 7-year period are to be received.