Answer: a=1, b=-1, c=1
D=3i and quadratic function will not intersect x-axis.
Explanation:
We have a quadratic function

or
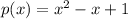
This is of the form:
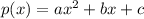
comparing the co-efficients of the two equations,
a=1, b=-1, c=1
Discriminant
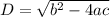
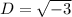 i.e D=3i
i.e D=3i
where
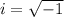
A quadratic function can have at-most of two roots. i.e, it can intersect x-axis, at 2 distinct points, or 1 identical point or not intersect at all.
This can be seen from the value of it's discriminant.
If D>0 ; Equation will have 2 distinct roots.
If D=0 ; Both the roots of the equation are equal and 1 point of intersection
If D<0 ; Roots are imaginary and function will not intersect x-axis.
Here, D<0, and quadratic function will not intersect x-axis.