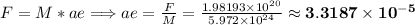Question

Let r denote the distance between the center of the earth and the center of the moon. What is the magnitude of the acceleration ae of the earth due to the gravitational pull of the moon?

Answer 1

The magnitude of the acceleration ae of the earth due to the gravitational pull of the moon is
`\mathbf{3.3187*10^(-5)}(m)/(s^(2))`

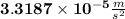
Step-by-step explanation:

By Newton's gravitational law, the magnitude of the gravitational force between two objects is:

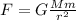`F=G(Mm)/(r^(2))`(1)

With G the gravitational constant, M the mass of earth, m the mass of the moon and r the distance between the moon and the earth, a quick search on physics books or internet websites give us the values:

`M=5.972*10^(24)\,kg`

`m=7.34767309*10^(22)\,kg`

`r=384400\,km`

`G=6.674*10^(-11)\,(N\,m^(3))/(kg^(2))`

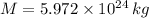
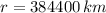
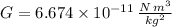
Using those values on (1)

`F=(6.674*10^(-11))*((5.972*10^(24))(7.34767309*10^(22)))/((384400*10^(3))^(2))`

`F\approx1.98193*10^(20)N`

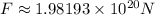
Now, by Newton's second Law we can find the acceleration of earth ae due moon's pull:

`F=M*ae\Longrightarrow ae=(F)/(M)=(1.98193*10^(20))/(5.972*10^(24))\approx\mathbf{3.3187*10^(-5)}`