Answer:
The sides of the container should be 3 cm and height should be 6 cm to minimize the cost
Explanation:
Data provided in the question:
costs for the material used on the side = $3/cm²
costs for the material used for the top lid and the base = $6/cm²
Volume of the container = 54 cm³
Now,
let the side of the base be 'x' and the height of the box be 'y'
Thus,
x × x × y = 54 cm³
or
x²y = 54
or
y =
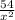 ............(1)
............(1)
Now,
The total cost of material, C
C = $3 × ( 4 side area of the box ) + $6 × (Area of the top and bottom)
or
C = ( $3 × 4xy ) + ( $6 × (x²) )
substituting the value of y in the above equation, we get
C =
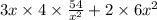
or
C =
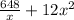
Differentiating with respect to x and putting it equals to zero to find the point of maxima of minima
thus,
C' =
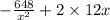 = 0
= 0
or
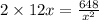
or
24x³ = 648
or
x = 3 cm
also,
C'' =
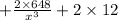
or
C''(3) =
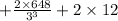 > 0
> 0
Hence,
x = 3 cm is point of minima
Therefore,
y =
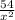 [from 1]
[from 1]
or
y =
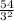
or
y = 6 cm
Hence,
The sides of the container should be 3 cm and height should be 6 cm to minimize the cost