Question

The Hypotenuse of a right triangle is 0.5 units long. The longer leg is 0.1 units longer than the shorter leg. Find the lengths of the sides of the triangle.​

Answer 1

The lengths of the sides of a right triangle are

Longer leg = 0.4 units.

Shorter leg = 0.3 units.

Explanation:

Given:

Hypotenuse = 0.5 units

Let the length of shorter leg of right triangle be x units then

According to the given condition,

length of longer leg will be (0.1 + x) units

Now,we know for a right triangle,by Pythagoras theorem we have

`(\textrm{Hypotenuse})^(2) = (\textrm{Longer leg})^(2)+(\textrm{Shorter leg})^(2)`

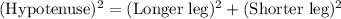
substituting the values we get

`0.5^(2)= (x+0.1)^(2)+ x^(2)`

Applying
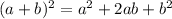`(a+b)^(2)= a^(2)+2ab+b^(2)` we get

`0.25= x^(2) +2* 0.1* x+ 0.1^(2) + x^(2) \\2x^(2) +0.2x+0.01-0.25=0\\2x^(2) +0.2x-0.24=0\\`

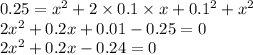
which is a quadratic equation

dividing the equation throughout by two we get

`x^(2) +0.1x-0.12=0\\\textrm{on factorizing we get}\\x^(2) +0.4x-0.3x-0.12=0\\(x+0.4)(x-0.3)=0`

`\therefore (x-0.3)= 0\\\therefore x=0.3`

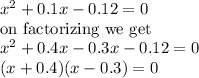
Since x cannot be negative we take

x = 0.3 units

∴ Longer leg = x + 0.1

= 0.3+0.1

=0.4 units

So, the lengths of the sides of a right triangle are

Longer leg = 0.4 units.

Shorter leg = 0.3 units.