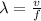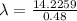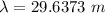Answer:
1.

2.
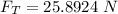
3.
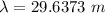
Step-by-step explanation:
Given:
- mass of slinky,
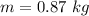
- length of slinky,
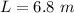
- amplitude of wave pulse,
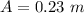
- time taken by the wave pulse to travel down the length,
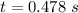
- frequency of wave pulse,
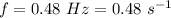
1.

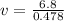

2.
Now, we find the linear mass density of the slinky.
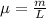
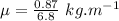
We have the relation involving the tension force as:
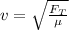
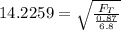

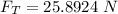
3.
We have the relation for wavelength as: