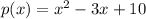Question

Eeeeee I’m so confused, i is needs help

Answer 1

The needed quadratic equation is :
`p(x) = x^2 -3x + 10`

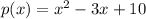
Explanation:

The given equation is of the form
`p(x) = ax^2 + bx + c`

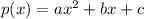
The given solutions of the equations are:

x = 3 +i, x = 3 - i

Now, if x = a is the zero of the polynomial p(x)

⇒(x -a ) is the root of the given polynomial.

⇒ (x - ( 3+i)) and (x - ( 3+i)) are the given roots for p(x)

P(X) = PRODUCT OF ALL ROOTS

⇒ p(x) = (x - ( 3+i))(x - ( 3-i)) = ( x-3 -i)(x -3+i)

Now,
`(a-b)(a +b) = a^2 - b^2\\\implies ( (x-3)-i)((x-3)+i) = (x-3)^2 - (i)^2 = x^2 +9 - 3x -(-1)\\= x^2 +10 - 3x\\\implies p(x) = x^2- 3x + 10`

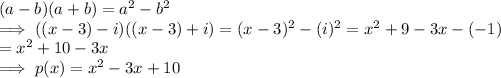
Hence, the needed quadratic equation is :
`p(x) = x^2 -3x + 10`