Answer:
To conduct the hypothesis test I would use the standard normal distribution to calculate the critical value and the p-value.
Explanation:
To conduct the hypothesis test I would use the standard normal distribution because there is a large sample size of n = 125 households. This because a point estimator for the true proportion p of one-person households is
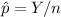 which is normally distributed with mean p and standard error
which is normally distributed with mean p and standard error
 when the sample size n is large. Here Y is the random variable that represents the number of one-person households observed. Then the test statistic is
when the sample size n is large. Here Y is the random variable that represents the number of one-person households observed. Then the test statistic is
 which has a standard normal distribution under the null hypothesis.
which has a standard normal distribution under the null hypothesis.