Question

Geoff has been running a restaurant in the city for many years. He knows from experience that the proportion of customers that leave tips at this restaurant is 0.56. Geoff has recently opened a restaurant in a suburban area. It seems that tipping habits are different in the suburbs: Geoff believes that the proportion of customers that tip at his new restaurant (p) may be different to 0.56. He conducts a hypothesis test to find out. The null and alternative hypotheses are: H0: p = 0.56 Ha: p ≠ 0.56 Geoff takes a random sample of 113 customers and notes whether or not they leave a tip. In this sample, the proportion of people that leave a tip is 0.60. a)Calculate the test statistic (z). Give your answer to 2 decimal places. z = 0.857 b)Calculate the P-value. Give your answer as a decimal to 4 decimal places. P-value = 0.3898

Answer 1

(a) 0.87 (b) 0.3843

Explanation:

We have the null and alternative hypotheses
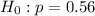`H_(0): p = 0.56` and
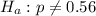`H_(a): p\\eq 0.56` (two-tailed alternative). There is a large sample size of n = 113 customers and a point estimate of p that is
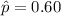`\hat{p} = 0.60` with an estimate standard deviation given by
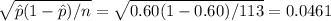`\sqrt{\hat{p}(1-\hat{p})/n} = √(0.60(1-0.60)/113) = 0.0461`. Then, the test statistic z which comes from a standard normal distribution is given by

(a)
`z = \frac{\hat{p}-0.56}{\sqrt{\hat{p}(1-\hat{p})/n}}=(0.60-0.56)/0.0461 = 0.8677`

(b) The p-value is given by 2P(Z > 0.87) = 0.3843, this because we are dealing with a two-tailed alternative.