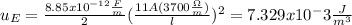Answer:
a)
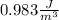
b)
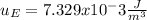
Step-by-step explanation:
The energy density is "the energy per unit volume, in the electric field. The energy stored between the plates of the capacitor equals the energy per unit volume stored in the electric field times the volume between the plates".
A magnetic field is a "vector field that describes the magnetic influence of electric charges in relative motion and magnetized materials".
Part a
For this case we can assume use the equation for the magnetic field in terms of the energy per unit of volume.
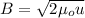
Where μ0 represent the permeability constant, also known as the magnetic constant. If we solve for u we got:
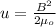
We also know that the magnetic field can be expressed in terms of the current and the radius of action R like this:
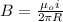
Replacing this on the formula for u we have:

And simplyfing we got:
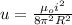
Replacing the values given we have:
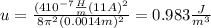
Part b
The density current is given by this formula
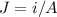 and the resistance by
and the resistance by
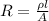
If we use the equation for the energy density we have this:
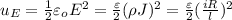
And replacing the values given we have: