Question

Two ice skaters collide on the ice. A 39.6-kg skater moving South at 6.21 m/s collides with a 52.1-kg skater moving East at 4.33 m/s. The two skaters entangle and move together across the ice. Determine the magnitude and direction of their post-collision velocity.

Answer 1

V = 3.6385 m/s

θ = 47.46 degrees

Step-by-step explanation:

the important data in the question is:

Skater 1:

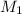`M_1`= 39.6 kg

direction: south (axis y)

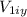`V_(1iy)` = 6.21 m/s

Skater 2:

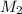`M_2` = 52.1 kg

direction: east (axis x)

`V_(2ix)` = 4.33 m/s

Now using the law of the conservation of linear momentum (
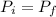`P_i = P_f` and knowing that the collision is inelastic we can do the next equations:

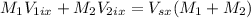`M_(1)V_(1ix)+M_2V_(2ix) = V_(sx)(M_1+M_2)` (eq. 1)

`M_(1)V_(1iy)+M_2V_(2iy) = V_(sy)(M_1+M_2)` (eq. 2)

Where
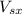`V_(sx)` and
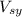`V_(sy)` is the velocity of the sistem in x and y after the collision.

Note: the conservation of the linear momentum have to be make once by each axis.

Now, in the (eq. 1) the skater 1 don't have velocity in the axis x, so we can replace
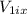`V_(1ix)` by 0 in the equation and get:

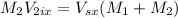`M_2V_(2ix) = V_(sx)(M_1+M_2)` (eq. 1)

also, in the (eq. 2) the skater 2 don't have velocity in the axis y, so we can replace
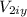`V_(2iy)` by 0 in the equation and get:

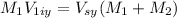`M_(1)V_(1iy) = V_(sy)(M_1+M_2)` (eq. 2)

Now, we just replace the data in both equations:

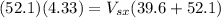`(52.1)(4.33) = V_(sx)(39.6+52.1)` (eq. 1)

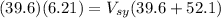`(39.6)(6.21) = V_(sy)(39.6+52.1)` (eq. 2)

solving for
`V_{sx]` and
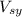`V_(sy)` we have:

`V_{sx]` = 2.46 m/s

`V_{sy]` = 2.681 m/s

using the pythagoras theorem we can find the magnitude of the velocity as:

V =
`√(2.46^2+2.681^2)`

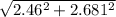
V = 3.6385 m/s

For find the direction we just need to do this;

θ =
`tan^(-1)((2.681)/(1.46))`

θ = 47.46 degrees