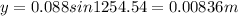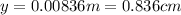Question

What is the equation describing the motion of a mass on the end of a spring which is stretched 8.8 cm from equilibrium and then released from rest, and whose period is 0.66 s?

Assume that the displacement at the start of the motion is positive.
What will be its displacement after 2.3 s ?

Answer 1

`0.836cm` in the positive direction.

Explanation:

The equation that describes the motion of this mass-spring system is given by;

`y=Asin\omega t...................(1)`

Where A is the amplitude, which defined as the maximum displacement from the equilibrium position for a body in simple harmonic motion.

`\omega` is the angular velocity measured in
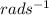`rads^{-1`, this is the angle turned through per unit time.

`y` is the displacement along the axis of the amplitude, and
`t` is any instant of time in the motion.

Given; A = 8.8cm = 0.088m

The angular velocity is given by the following relationship also;

`\omega=2\pi/T`

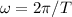
Where T is the period, which is defined as the time taken for a body in simple harmonic motion to make one complete oscillation.

Given; T=0.66s

Therefore;

`\omega=2\pi/0.66\\\omega=3.03\pi rads^{-1`

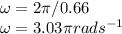
Substituting all values into equation (1) we obtain the following;

`y=0.088sin3.03\pi t................(2)`

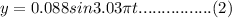
Equation (2) is the equation describing the motion of the mass on the spring.

At an instant of time t = 2.3s, the displacement is therefore given as follows;

`y=0.088sin[3.03\pi(2.3)]\\y=0.088sin6.97\pi\\`

By conversion,
`6.97\pi rad=6.97*180^o=1254.55^o`

Therefore

`y=0.088sin1254.54=0.00836m\\`

`y=0.00836m=0.836cm`