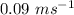Question

A thread holds two carts together on a frictionless surface. A spring is compressed

between the two carts. After the thread between the two carts is cut the cart on the
left with a mass of 1.5 kg moves away with a velocity of 27 cm/s. What is the
velocity of the cart on the right that has a mass of 4.5 kg? thisss is the answer I just need to show work>>>>>>>(0.09 m/s)

Answer 1

Velocity on the right side of the cart
`=0.09\ ms^(-1)`

Step-by-step explanation:

Given

⇒The mass on the left of the cart
`m_1=1.5\ kg`

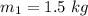
Its velocity
`v_1=27\ cm/s`,
`v_1=(27)/(100)=0.27\ m/s`

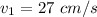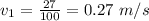
⇒Mass on the right of the cart
`m_2=4.5\ kg`

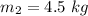
Velocity
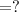`=?` We have to find
`v_2`

From

The law of conservation of linear momentum:

We can say that.

Initial momentum will equalize the final momentum.

And momentum is the product of mass and its velocity.

Assigning one of its velocity as negative because both are in different direction.

Lets call
`v_1=-0.27m/s`

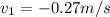
Recalling the formula and plugging the values.

`m_1(-v_1)+m_2v_2=0`

`v_2=-(m_1(-v_1))/(m_2) =-(1.5* -0.27)/(4.5) =0.09\ m/s`

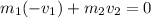
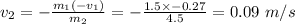
So the velocity of the cart on the right side that has a mass of
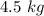`4.5\ kg` is
`0.09\ ms^(-1)`