Answer:
The final velocity of the first glider is 3.39553 m/s in the opposite direction
The final velocity of the second glider is 0.31553 m/s in the same direction
Step-by-step explanation:
 = Mass of first glider = 0.14 kg
= Mass of first glider = 0.14 kg
 = Mass of second glider = 0.299 kg
= Mass of second glider = 0.299 kg
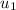 = Initial Velocity of first glider = 0.8 m/s
= Initial Velocity of first glider = 0.8 m/s
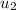 = Initial Velocity of second glider = -2.28 m/s
= Initial Velocity of second glider = -2.28 m/s
 = Final Velocity of first glider
= Final Velocity of first glider
 = Final Velocity of second glider
= Final Velocity of second glider
As momentum and Energy is conserved

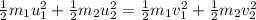
From the two equations we get
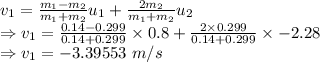
The final velocity of the first glider is 3.39553 m/s in the opposite direction
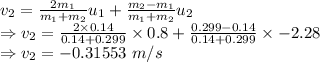
The final velocity of the second glider is 0.31553 m/s in the same direction