Question

In designing a backyard water fountain, a gardener wants to stream of water to exit from the bottom of one tub and land in a second one. The top of the second tub is 0.5 m below the hole in the first tub, which has water in it to a depth of 0.15 m. How far to the right of the first tub must the second one be placed to catch the stream of water?

Answer 1

To solve this problem it is necessary to apply the concepts related to the kinematic equations of movement description.

From the definition we know that the speed of a body can be described as a function of gravity and height

`V = √(2gh)`

`V = √(2*9.8*0.15)`

`V = 1.714m/s`

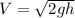
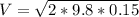
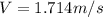
Then applying the kinematic equation of displacement, the height can be written as

`H = (1)/(2)gt^2`

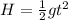
Re-arrange to find t,

`t = \sqrt{2(h)/(g)}`

`t = \sqrt{2(0.5)/(9.8)}`

`t = 0.3194s`

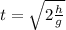
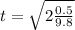
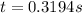
Thus the calculation of the displacement would be subject to

`x = vt`

`x =1.714*0.3194`

`x = 0.547m`

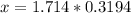
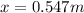
Therefore the required distance must be 0.547m