Question

For lunch you and your friends decide to stop at the nearest deli and have a sandwich made fresh for you with 0.100kg{\rm kg} of turkey. The slices of turkey are weighed on a plate of mass 0.400kg{\rm kg} placed atop a vertical spring of negligible mass and force constant of 200N/m{\rm N/m} . The slices of turkey are dropped on the plate all at the same time from a height of 0.250m{\rm m} . They make a totally inelastic collision with the plate and set the scale into vertical simple harmonic motion (SHM). You may assume that the collision time is extremely small.What is the amplitude of oscillations A of the scale after the slices of turkey land on the plate?

Answer 1

0.02268 m

Step-by-step explanation:

`m_1` = Mass of turkey slices = 0.1 kg

`m_2` = Mass of plate = 0.4 kg

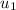`u_1` = Initial Velocity of turkey slices = 0 m/s

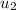`u_2` = Initial Velocity of plate = 0 m/s

`v_1` = Final Velocity of turkey slices

`v_2` = Final Velocity of plate

k = Spring constant = 200 N/m

x = Compression of spring

g = Acceleration due to gravity = 9.81 m/s²

Equation of motion

`v^2-u^2=2as\\\Rightarrow v=√(2as+u^2)\\\Rightarrow v=√(2* 9.81* 0.25+0^2)\\\Rightarrow v=2.21472\ m/s`

The final velocity of the turkey slice is 2.21472 m/s = v₁

For the spring

`x=(m_1g)/(k)\\\Rightarrow x=(0.1* 9.81)/(200)\\\Rightarrow x=0.004905\ m`

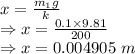
As the linear momentum is conserved

`m_1v_1=(m_1+m_2)v_2\\\Rightarrow v_2=(m_1v_1)/(m_1+m_2)\\\Rightarrow v_2=(0.1* 2.21472)/(0.1+0.4)\\\Rightarrow v_2=0.442944\ m/s`

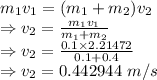
Here the kinetic and potential energy of the system is conserved

`(1)/(2)(m_1+m_2)v_2^2+(1)/(2)kx^2=(1)/(2)kA^2\\\Rightarrow A=\sqrt{((m_1+m_2)v_2^2+kx^2)/(k)}\\\Rightarrow A=\sqrt{((0.1+0.4)0.442944^2+200* 0.004905^2)/(200)}\\\Rightarrow A=0.02268\ m`

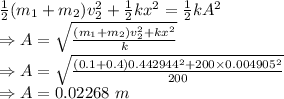
The amplitude of oscillations is 0.02268 m