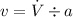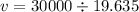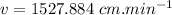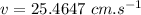Answer:
a)
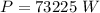
b)
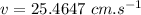
Step-by-step explanation:
Given:
- initial temperature of water,
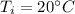
- volume flow rate of water in to the heating section,
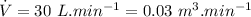
∵1L of water = 1 kg by mass
∴
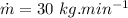
- final temperature of water,
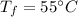
- diameter of insulated pipe,
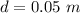
(a)
we have,
Specific heat capacity of water,
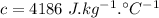
The amount of heat to be supplied per min to the water:
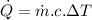
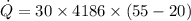

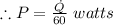
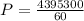
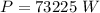
∴Power required is 73.225 kW.
(b)
∵Volume flow rate,
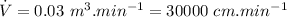
Now area of pipe:
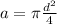
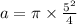
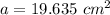
∴Flow velocity