Question

Assume that the heights of men are normally distributed with a mean of 66.9 inches and a standard deviation of 2.1inches. If 36 men are randomly selected, find the probability that they have a mean height greater than 67.9 inches.

A. 0.0021
B. 0.0210
C. 0.9979
D. 0.9005

Answer 1

A. 0.0021

Explanation:

Given that the heights of men are normally distributed with a mean of 66.9 inches and a standard deviation of 2.1inches.

Sample size = 36

Std dev of sample =
`(2.1)/(√(36) ) =0.35`

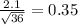
The sample entries X the heights are normal with mean= 66.9 inches and std deviation = 0.35 inches

Or we have

Z =
`(x-66.9)/(0.35)`

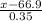
Hence the probability that they have a mean height greater than 67.9 inches

=
`P(X>67.9)\\=P(Z>(1)/(0.35)) \\=0.00214`

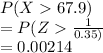
So option A is right answer.