Question

In order for a satellite to move in a stable circular orbit of radius 6588km at a constant speed, its centripetal acceleration must be inversely proportional to the square of the radius r of the orbit. What is the speed of the satellite and the time required to complete one orbit? The universal gravitational constant is 6.67259e-11 Nm^2/kg^2 and the mass of the earth is 5.98e24kg.

Answer 1

Step-by-step explanation:

Given that,

Radius in which the satellite orbits, r = 6588 km

Solution,

The centripetal force acting on the satellite is balanced by the gravitational force acting between earth and the satellite. Its expression can be written by :

`(GmM)/(r^2)=(mv^2)/(r)`

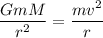
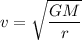`v=\sqrt{(GM)/(r)}`, M is the mass of earth

`v=\sqrt{(6.67259* 10^(-11)* 5.98* 10^(24))/(6588* 10^3)}`

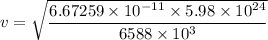
v = 7782.53 m/s

Let t is the time required to complete one orbit. It can be calculated as :

`t=(d)/(v)`

`t=(2\pi r)/(v)`

`t=(2\pi * 6588* 10^3)/(7782.53)`

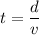
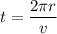
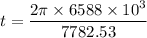
t = 5318.78 seconds

or

t = 1.47 hour

Therefore, this is the required solution.