Answer:
Complete question is attached with.
Both the triangles are congruent by ASA property of congruence and the segment RT is congruent to FD.
Explanation:
From angle sum property of the triangle we can find the measure of the missing angles.
As for
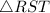 we can find
we can find
 which is
which is
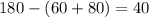
And for
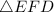 we can find
we can find
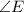 which is
which is
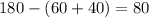
To find the congruence.
We see that
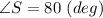 and
and
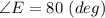
Then
 along with
along with
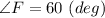
Between these two angles we have a segment that is equal in measure.
So two angles and a side in continuation, we can apply ASA property of congruence.
Now segment
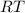 and segemnt
and segemnt
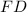 are congruent as both the segment have equal measures on it.
are congruent as both the segment have equal measures on it.
So finally option A is the correct choice and both the triangles are congruent by ASA property.
And RT is congruent with FD.