Question

An airplane propeller is 2.68 m in length (from tip to tip) and has a mass of 107 kg. When the airplane's engine is first started, it applies a constant torque of 1930 Nm to the propeller, which starts from rest.

a. What is the angular acceleration of the propeller? Treat the propeller as a slender rod.
b. What is the propeller's angular speed after making 5.00 rev?
c. How much work is done by the engine during the first 5.00 rev?
d. What is the average power output of the engine during the first 5.00 rev?
e. What is the instantaneous power output of the motor at the instant that the propeller has turned through 5.00 rev?

Answer 1

a)30.14 rad/s2

b)43.5 rad/s

c)60633 J

d)42 kW

e)84 kW

Step-by-step explanation:

If we treat the propeller is a slender rod, then its moments of inertia is

`I =(mL^2)/(12) = (107*2.68^2)/(12) = 64.04 kgm^2`

a. The angular acceleration is Torque divided by moments of inertia:

`\alpha = (T)/(I) = (1930)/(64.04) = 30.14 rad/s^2`

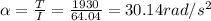
b. 5 revolution would be equals to
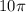`10\pi` rad, or 31.4 rad. Since the engine just got started

`\omega^2 = 2\alpha\theta = 2*30.14*31.4 = 1893.5`

`\omega = √(1893.5) = 43.5 rad/s`

c. Work done during the first 5 revolution would be torque times angular displacement:

`W = T*\theta = 1930 * 31.4 = 60633 J`

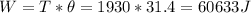
d. The time it takes to spin the first 5 revolutions is

`t = (\omega)/(\alpha) = (43.5)/(30.14) = 1.44 s`

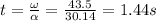
The average power output is work per unit time

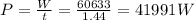`P = (W)/(t) = (60633)/(1.44) = 41991 W` or 42 kW

e.The instantaneous power at the instant of 5 rev would be Torque times angular speed at that time:

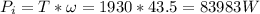`P_i = T*\omega = 1930*43.5=83983 W` or 84 kW