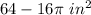Question

Four circles, each with a radius of 2 inches, are removed

from a square. What is the remaining area of the square?
(16 - 47T) in.?
(16 – ) in.
(64 - 167T) in.?
(64 - 4TT) in.?

Answer 1

C. on Edge

Explanation:

I just took the test

Answer 2

`(64-16\pi) in.`

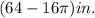
Explanation:

Given:

radius = 2 in.

Since 4 circles are circumscribed by a square, then the side length of the square is 8

Area of Square =
`side^2=8^2=64in^2`

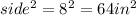
Area of 1 circle =
`2* \pi * r = 2\pi2=4\pi`

Area of 4 circles = 4 × Area of 1 Circle =
`4 * 4\pi=16\pi`

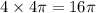
According to the question, these four circle are removed by the above square.

Therefore, Remaining Area of the square after removing these four circle= Area of the square- area of 4 circles =
`64-16\pi \ in^2`

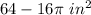
Hence Area of remaining square is
`64-16\pi \ in^2`