Question

A large wooden turntable in the shape of a flat uniform disk has a radius of 2.00 m and a total mass of 120 kg. The turntable is initially rotating at 3.00 rad>s about a vertical axis through its center. Suddenly, a 70.0-kg parachutist makes a soft landing on the turntable at a point near the outer edge. (a) Find the angular speed of the turntable after the parachutist lands. (Assume that you can treat the parachutist as a particle.) (b) Compute the kinetic energy of the system before and after the parachutist lands. Why are these kinetic energies not equal

Answer 1

a)1.385 rad/s

b) Before: 1080 J. After 498.46 J

Step-by-step explanation:

The moments of inertia of the turn table, with the shape of uniform disk is:

`I_1 = 0.5mr^2 = 0.5*120*2^2 = 240 kgm^2`

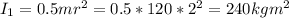
The angular momentum of the turn table before the impact is

`A_1 = \omega_1I_1 = 3*240 = 720 radkgm^2`

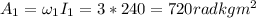
The moments of inertia of the system after the impact is (treating the parachute man is a point particle)

`I_2 = I_1 + Mr^2 = 240 + 70*2^2 = 240 + 280 = 520 kgm^2`

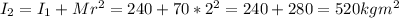
According to angular momentum conservation law:

`A_1 = A_2`

`720  = \omega_2I_2`

`\omega_2 = (720)/(I_2) = (720)/(520) = 1.385 rad/s`

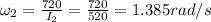
(b) Before the impact:

`K_1 = 0.5*I_1*\omega_1^2 = 0.5*240*3^2 = 1080 J`

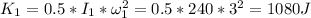
After the impct

`K_2 = 0.5*I_2*\omega_2^2 = 0.5*520*1.385^2 = 498.46 J`

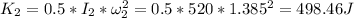
The kinetic energies are not equal because the impact is causing the turn table to lose energy.