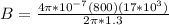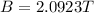To solve this problem it is necessary to apply the concepts related to Magnetic field in a toroide.
By definition the magnetic field is defined as
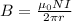
Where,
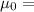 Permeability constant in free Space
Permeability constant in free Space
N = Number of loops
I = Current
r = Radius
PART A) For the internal radio,
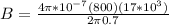
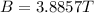
PART B) For outside radio,