Question

Elizabeth is a busy pediatrician. On any given day, she diagnoses an average of four babies with middle-ear infections. Assume that the number of babies who come to her clinic with middle-ear infections is a Poisson random variable. Calculate the probability that fewer than three babies with middle-ear infections will come to her clinic tomorrow. Give your answer in decimal form precise to three decimal places. P(X<3)=

Answer 1

There is a 23.81% probability that fewer than three babies with middle-ear infections will come to her clinic tomorrow.

Explanation:

In a Poisson distribution, the probability that X represents the number of successes of a random variable is given by the following formula:

`P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)`

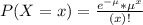
In which

x is the number of sucesses

e = 2.71828 is the Euler number

`\mu` is the mean in the given interval.

In this problem

Elizabeth is a busy pediatrician. On any given day, she diagnoses an average of four babies with middle-ear infections. This means that
`\mu = 4`.

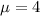Calculate the probability that fewer than three babies with middle-ear infections will come to her clinic tomorrow.

So

`P(X < 3) = P(X = 0) + P(X = 1) + P(X = 2)`

`P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)`

`P(X = 0) = (e^(-4)*4^(0))/((0)!) = 0.0183`

`P(X = 1) = (e^(-4)*4^(1))/((2)!) = 0.0733`

`P(X = 2) = (e^(-4)*4^(2))/((2)!) = 0.1465`

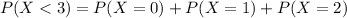
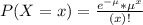
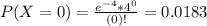
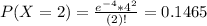
So

`P(X < 3) = P(X = 0) + P(X = 1) + P(X = 2) = 0.0183 + 0.0733 + 0.1465 = 0.2381`

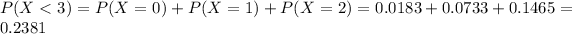
There is a 23.81% probability that fewer than three babies with middle-ear infections will come to her clinic tomorrow.