Question

a shower stall measures 86.0 cm x 86.0 cm x 210 cm. When you sing in the shower, which frequencies will sound the riches (because of resonance)

Answer 1

Step-by-step explanation:

From the given information:

The length of the shower stall L = 86.0 cm = 0.86 m

The width of the shower stall W = 210 cm = 2.1 m

Let assume that the stall acts as a closed pipe and the various singer voices range from 130 Hz to 2000 Hz.

Then; using wavelength equation;

`\lambda = 2 L`

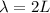
where;

`permitted \ sounds \ L = ( (n \lambda )/(2))` &

`v = f \lambda`

`\lambda = (v)/(f)`

∴

`L = (nv)/(2f) \ \ \ ... where, n = 1,2,3...`

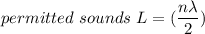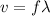
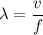
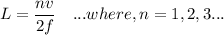
By making the resonating frequency f the subject of the above formula, we have:

`f_n = (nv)/(2L)`

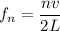
where;

L = 0.860 m , then n = 1

Thus;

`f_1 = (355 \ m/s * 1)/(2(0.860 \ m) )`

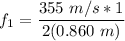
f = 206 Hz

For n = 9

`f_9 = (355 \ m/s * 9)/(2(0.860 \ m) )`

`f_9 = (3195)/( 1.72)`

`f_9 = 1857.56 \ Hz`

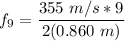
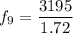
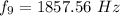
Thus, the resonant frequencies range for n = 1 to 9 with W = 2.10 m

However;

For n = 2

`f_2 = (355 \ m/s * 2)/(2(2.10 \ m) )`

`f_9 = 169 \ Hz`

For n = 23

`f_(23) = (355 \ m/s * 23 )/(2(2.10 \ m) )`

`f_(23) = 1944 \ Hz`

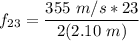
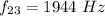
Thus, the resonant frequencies range from n = 2 to n= 23.