Question

Find a recurrence relation for the number of pairs of rabbits after n months if (1) initially there is one pair of rabbits who were just born, and (2) every month each pair of rabbits that are over one month old have a pair of offspring (a male and a female).

Answer 1

The recurrence relation for the number of pairs of rabbits after n months is R(n) = R(n-1) + R(n-2) for n > 2.

Step-by-step explanation:

To find a recurrence relation for the number of pairs of rabbits after n months, we can observe that each pair of rabbits that are over one month old will give birth to a new pair of offspring. Let's denote the number of pairs of rabbits after n months as R(n). After the first month, the initial pair of rabbits gives birth to one pair of offspring, so R(1) = 1. After the second month, the initial pair of rabbits is still not mature enough to give birth, so R(2) = 1. But after the third month, the initial pair of rabbits will give birth to another pair, and the first pair of offspring will also become mature enough to give birth, resulting in a total of three pairs of rabbits. So, R(3) = 3.

We can see that the number of pairs of rabbits after each month is equal to the sum of the number of pairs of rabbits in the previous two months. This can be represented as the recurrence relation:

R(n) = R(n-1) + R(n-2) for n > 2

Answer 2

Relation :
`(F_(N))/(F_(N-1) )`

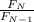
Ratio reaches limit at value : 1.61803398

Step-by-step explanation:

To solve this, we need to use the Fibonacci Sequence.

Let F(n) be the number of pair of rabbits after n months.

At 0 month , we have 0 pair of rabbit.

Initially we have 1 pair of rabbit that was just born so , at 1 month , we have 1 pair of rabbit

F(1) = 1

And next month another pair of rabbit is born so:

F(2) = 1

As given, each pair of rabbit gives birth to another pair of rabbit after a month so :

After 3 months, the rabbits will be as follows:

Initial pair ----> Gives 1 pair

2nd pair -----> Gives 1 pair

New pair of rabbits now = 1+1 = 2

So to write this in terms of n, we can simply write it as :

F(n) = F(n-1) +F(n-2)

Which gives the value of rabbits after 'n' months

We can also do this using successive term ratio which gives us the recurrence relation for pairs of rabbits after n months:

for n month, the ratio will be equal to
`(F_(N))/(F_(N-1) )`

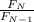
Using Excel, and by starting at month 2 to avoid dividing by zero, we see that ratio reaches limit of 1.61803398