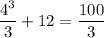Answer:
See below
Explanation:
We start by dividing the interval [0,4] into n sub-intervals of length 4/n
![[0,\displaystyle(4)/(n)],[\displaystyle(4)/(n),\displaystyle(2*4)/(n)],[\displaystyle(2*4)/(n),\displaystyle(3*4)/(n)],...,[\displaystyle((n-1)*4)/(n),4]](https://img.qammunity.org/2020/formulas/mathematics/college/77g5wts7r1kdzmkgwh0krx2jkr33fk8htz.png)
Since f is increasing in the interval [0,4], the upper sum is obtained by evaluating f at the right end of each sub-interval multiplied by 4/n.
Geometrically, these are the areas of the rectangles whose height is f evaluated at the right end of the interval and base 4/n (see picture)

but
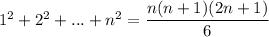
so the upper sum equals
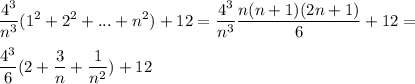
When
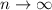 both
both
 and
and
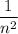 tend to zero and the upper sum tends to
tend to zero and the upper sum tends to