Question

Solve the equation by graphing. If exact roots cannot be found, state the consecutive integers between which the roots are located. x^2 + 5x + 4 = 0

Answer 1

The equation contains exact roots at x = -4 and x = -1.

See attached image for the graph.

Explanation:

We start by noticing that the expression on the left of the equal sign is a quadratic with leading term
`x^2`, which means that its graph shows branches going up. Therefore:

1) if its vertex is ON the x axis, there would be one solution (root) to the equation.

2) if its vertex is below the x-axis, it is forced to cross it at two locations, giving then two real solutions (roots) to the equation.

3) if its vertex is above the x-axis, it will not have real solutions (roots) but only non-real ones.

So we proceed to examine the vertex's location, which is also a great way to decide on which set of points to use in order to plot its graph efficiently:

We recall that the x-position of the vertex for a quadratic function of the form
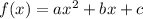`f(x)=ax^2+bx+c` is given by the expression:
`x_v=(-b)/(2a)`

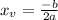
Since in our case
`a=1` and
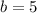`b=5`, we get that the x-position of the vertex is:
`x_v=(-b)/(2a) \\x_v=(-5)/(2(1))\\x_v=-(5)/(2)`

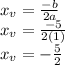
Now we can find the y-value of the vertex by evaluating this quadratic expression for x = -5/2:

`y_v=f(-(5)/(2))\\y_v=(-(5)/(2) )^2+5(-(5)/(2) )+4\\y_v=(25)/(4) -(25)/(2) +4\\\\y_v=(25)/(4) -(50)/(4)+(16)/(4) \\y_v=-(9)/(4)`

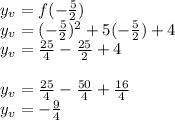
This is a negative value, which points us to the case in which there must be two real solutions to the equation (two x-axis crossings of the parabola's branches).

We can now continue plotting different parabola's points, by selecting x-values to the right and to the left of the
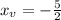`x_v=-(5)/(2)`. Like for example x = -2 and x = -1 (moving towards the right) , and x = -3 and x = -4 (moving towards the left.

When evaluating the function at these points, we notice that two of them render zero (which indicates they are the actual roots of the equation):

`f(-1) = (-1)^2+5(-1)+4= 1-5+4 = 0\\f(-4)=(-4)^2+5(-4)_4=16-20+4=0`

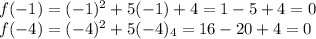
The actual graph we can complete with this info is shown in the image attached, where the actual roots (x-axis crossings) are pictured in red.

Then, the two roots are: x = -1 and x = -4.