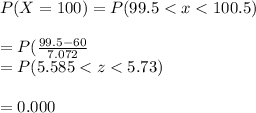Answer:
0.0000
Explanation:
Given that a die is rolled 360 times. Let say that you want to use normal approximation to find the probability that the number of 4 was rolled exactly 100 times.
Here we know that getting 4 is binomial with p = 1/6 and n =360
By approximating to normal after checking conditions are satisfied we have
X = no of fours obtained is normal
with mean =
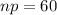
and variance =
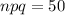
Std dev = 7.072
X is N(60, 7.072)
For finding out prob x=100 we have to do continuity correction as