Question

If the radius of a blood vessel drops to 84.0% of its original radius because of the buildup of plaque, and the body responds by increasing the pressure difference across the blood vessel by 10.0%, what will have happened to the flow rate? The flow rate will have changed to ...... % of its original value.

Answer 1

To develop this problem it is necessary to apply the equations concerning Bernoulli's law of conservation of flow.

From Bernoulli it is possible to express the change in pressure as

`\Delta P = (1)/(2)\rho (v_1^2-v_2^2)+ \rho g (h_1h_2)`

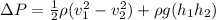
Where,

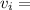`v_i =`Velocity

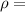`\rho =` Density

g = Gravitational acceleration

h = Height

From the given values the change of flow is given as

`R = r^4P`

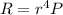
Therefore between the two states we have to

`(R_2)/(R_1) = (r_2^4 P_2)/(r_1^4 P_1) *100\%`

`(R_2)/(R_1) = (84^4 (110))/(100^4*(100)) *100\%`

`(R_2)/(R_1) = 54.77\%`

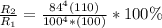
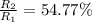
The flow rate will have changed to 54.77 % of its original value.