Question

Complete parts ​(a) through ​(c) below. ​(a) Determine the critical​ value(s) for a​ right-tailed test of a population mean at the alphaequals0.10 level of significance with 20 degrees of freedom. ​(b) Determine the critical​ value(s) for a​ left-tailed test of a population mean at the alphaequals0.10 level of significance based on a sample size of nequals15. ​(c) Determine the critical​ value(s) for a​ two-tailed test of a population mean at the alphaequals0.05 level of significance based on a sample size of nequals12. LOADING... Click here to view the​ t-Distribution Area in Right Tail.

Answer 1

a) The critical value on this case would be
`t_(crit)=1.325`

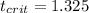
b) The critical value on this case would be
`t_(crit)=-1.345`

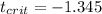
c) The critical values on this case would be
`t_(crit)=\pm 2.201`

Explanation:

Part a

The system of hypothesis on this case would be:

Null hypothesis:
`\mu \leq \mu_0`

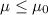
Alternative hypothesis:
`\mu > \mu_0`

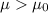
Where
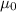`\mu_0` is the value that we want to test.

In order to find the critical value we need to find first the degrees of freedom, on this case that is given df=20. Since its an upper tailed test we need to find a value a such that:

`P(t_(20)>a) = 0.1`

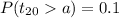
And we can use excel in order to find this value with this function: "=T.INV(0.9,20)". The 0.9 is because we have 0.9 of the area on the left tail and 0.1 on the right.

The critical value on this case would be
`t_(crit)=1.325`

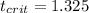
Part b

The system of hypothesis on this case would be:

Null hypothesis:
`\mu \geq \mu_0`

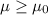
Alternative hypothesis:
`\mu < \mu_0`

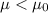
Where
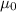`\mu_0` is the value that we want to test.

In order to find the critical value we need to find first the degrees of freedom, given by:

`df=n-1=15-1=14`

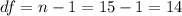
Since its an lower tailed test we need to find b value a such that:

`P(t_(14)<b) = 0.1`

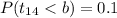
And we can use excel in order to find this value with this function: "=T.INV(0.1,14)". The 0.1 is because we have 0.1 of the area accumulated on the left of the distribution.

The critical value on this case would be
`t_(crit)=-1.345`

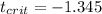
Part c

The system of hypothesis on this case would be:

Null hypothesis:
`\mu = \mu_0`

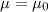
Alternative hypothesis:
`\mu \\eq \mu_0`

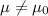
Where
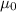`\mu_0` is the value that we want to test.

In order to find the critical value we need to find first the degrees of freedom, given by:

`df=n-1=12-1=11`

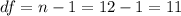
Since its a two tailed test we need to find c value a such that:

`P(t_(11)>c) = 0.025` or
`P(t_(11)<-c) = 0.025`

And we can use excel in order to find this value with this function: "=T.INV(0.025,11)". The 0.025 is because we have 0.025 of the area on each tail.

The critical values on this case would be
`t_(crit)=\pm 2.201`